复合微下击暴流风场下小型无人机的飞行分析

王文博; 李海城; 吴超; 车晓涛; 杜明磊

doi:10.15892/j.cnki.djzdxb.2025.01.003

PDF(5453 KB)

弹箭与制导学报 ›› 2025, Vol. 45 ›› Issue (1) : 17-25. DOI: 10.15892/j.cnki.djzdxb.2025.01.003

复合微下击暴流风场下小型无人机的飞行分析

作者信息 +

Flight Analysis of Small UAV Under Composite Micro-downburst Wind Field

Author information +

文章历史 +

摘要

为研究复合微下击暴流风场对轻小型固定翼无人机巡航段的影响,文中构建了Dryden大气紊流模型与微下击暴流风场模型,融合后得到复合微下击暴流风场,并以电动无人机为例,进行了六自由度刚体弹道模型仿真分析。仿真结果表明,所建立的复合风场具有较好的随机特性与典型的风切变特征,能够有效描述实际复合微下击暴流风场的分布及变化;在风场影响下,该电动无人机高度损失明显,在中心诱导速度为10~25 m/s时,损失高度达168~537 m;此外,无人机的航时、攻角、侧滑角以及动力余量等飞行参数亦发生了不同程度的变化。

Abstract

To study the influence of the composite microburst wind field on the cruise phase of a light and small fixed-wing unmanned aerial vehicle (UAV), in this paper, a Dryden atmospheric turbulence model and a microburst model are constructed, and after fusing them, a composite microburst wind field model is created. Take a specific electric-powered UAV as the object of study and carry out a six-degree-of-freedom rigid body ballistic model simulation analysis, the simulation results show that the newly established composite wind field model has better randomness and typical wind shear characteristics and it can effectively depict the actual composite microburst wind field distribution and change. Under the influence of this composite wind field, the UAV has experienced a significant loss of height, and when the central induced velocity is between 10~25 m per second, the loss of height reached 168~537 m. Furthermore, the flight parameters of UAV, including flight duration, angle of attack, sideslip angle, and power margin, have changed in different degree.

导出引用

王文博, 李海城, 吴超, 等. 复合微下击暴流风场下小型无人机的飞行分析[J]. 弹箭与制导学报, 2025, 45(1): 17-25 https://doi.org/10.15892/j.cnki.djzdxb.2025.01.003

WANG Wenbo, LI Haicheng, WU Chao, et al. Flight Analysis of Small UAV Under Composite Micro-downburst Wind Field[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2025, 45(1): 17-25 https://doi.org/10.15892/j.cnki.djzdxb.2025.01.003

中图分类号： TJ765.3 TP391.9

0 引言

在现代战场环境中,无人机因其高机动性、多样化作战能力、低造价成本,以及在快速反应和精确打击中的卓越表现,已成为打击时敏及高价值目标的重要作战平台。然而,作为一种小型低速飞行器,无人机的作战效能在复杂气象条件下,尤其是在极端天气中,受到显著限制。据研究,气象条件对传统弹药的射击精度有显著影响,其中气流变化是关键因素^[1]。相比之下,无人机因其飞行时间长、速度低、气动特性敏感,更易受到风切变和大气紊流的干扰,导致姿态失稳、任务失败以及精确打击能力下降。

目前,关于弹箭风场的建模大多采用简化的平均风模型和随机扰动风模型,但这些模型在处理复杂作战环境中的典型风场现象时存在一定的局限性。微下击暴流作为一种局地性极强的极端天气现象,是一种典型的风切变现象,常发生在我国西南一带与东南沿海^[2]等战略敏感地区,往往伴随着剧烈的垂直风切变,能够在短时间内产生强烈的下沉气流,严重威胁低空飞行器的稳定性和操控能力。这种难以预测的气象现象对无人机的飞行性能提出了严峻挑战,尤其是在复杂动态的战场态势中,传统的气象探测难以完全应对突发情况。因此,无人机在恶劣气象条件下保持可靠的飞行与打击性能,不仅是应对这些恶劣天气的关键,也是提高作战效果,实现出其不意战术优势的必要条件。

现有研究主要集中在大型航空器的气动性能分析和飞行稳定性影响方面,通过风洞实验与数值模拟探讨微下击暴流对商用客机和军用运输机的影响,并提出相应的应对策略。只有少部分在对诸如巡航导弹、制导火箭弹、火炮等传统弹药的研究,陈建伟等先后建立了低空风切变风场^[3],以尾翼火箭弹为对象进行弹道仿真,得到无控火箭弹在特定风场下的扰动规律^[4];王晋以涡环模型建立了微下击暴流风场,通过融合雨滴运动模型^[5]、结合位势流动理论^[6]对火炮外弹道特性进行偏差分析。然而,无人机在微下击暴流及其复合形式下的飞行特性研究较少。此外,无人机在穿越微下击暴流场时,常遇到不规则突风和湍流扰动^[7],这些因素共同作用,形成更为复杂的复合微下击暴流,使风场结构更加复杂,提高了飞行控制与路径规划的难度。因此,研究无人机在复杂风场环境下的飞行,具有重要的实际意义。为此,通过建立复合微下击暴流风场来模拟恶劣气象环境,其中包括典型的微下击暴流和大气紊流特征。相比于传统的随机扰动模型,该复合风场更具真实的三维流场特性与时间连续相关性,更真实反映了复杂作战场景中的气象条件。

文中以电动无人机的巡航段为例,对其在复合微下击暴流风场下的航迹、航时、能量消耗、攻角及侧滑角进行仿真分析,旨在为恶劣环境下无人机的总体设计和飞行控制优化提供新的思路与参考。

1 复合微下击暴流风场模型的建立

选取基于流体力学原理的涡环模型来构建微下击暴流风场,引入倾斜变化与涡环对叠加,实现实际风场中的三维特性与非对称性;基于随机平稳过程理论,建立Dryden模型,通过随机双交换法与相关性检验,实现大气紊流场的建立。通过无人机的时空特性将两者融合得到复合微下击暴流风场模型。

1.1 多倾斜涡环对风切变模型

在空间范围内,微下击暴流通常表现为如下的流动形式:高度300~1 000 m范围内,高压气旋(云层)中部形成一股向下的气流,气流撞击地面后,呈辐射状水平散开,并在外围形成尾流旋涡^[8]。强对流天气、锋面天气、低空急流及下击暴流均会产生风切变,图1为形成示意图。

图1 下击暴流形成示意图

Fig.1 Schematic diagram of downburst formation

Full size|PPT slide

多倾斜涡环对风切变模型是通过设置对称涡环对模拟单对涡环形成的下击暴流;再考虑由地形等引起的非对称性,使用坐标转移矩阵进行倾斜放置;最后结合实际应用场景的影响,适当对涡环位置进行调整。

1.1.1 对称涡环模型

建立涡环地面坐标系Oxyz,x,y,z依次指向北、东、天方向为正,以地面上方一点O_P为中心设置主涡环,其半径为R,涡环设置示意如图2。

图2 对称涡环对设置示意图

Fig.2 Schematic diagram of symmetrical vortex ring pair setup

Full size|PPT slide

该模型经解算后,对称涡环流线方程可表示为:

\begin{matrix} ψ = \frac{Γ}{2 π} (F_{p} (k) - F_{I} (k)) \end{matrix}

(1)

式中:

Г

为涡环强度;F_p(k),F_I(k)为点O_p,O_I处的椭圆积分函数,k为涡环线方程的椭圆积分自变量。Γ,F(k),k可表示为:

\begin{matrix} \{\begin{array}{l} Γ = 2 R v_{z} (0) \\ F (k) \approx \frac{0.788 k^{2} (r_{m a x} + r_{m i n})}{0.25 + 0.75 \sqrt{1 - k^{2}}} \\ k = |\frac{r_{m a x} - r_{m i n}}{r_{m a x} + r_{m i n}}| \end{array} \end{matrix}

(2)

式中:v_z(0)为涡环中心向下的诱导速度;R为涡环半径;r_max,r_min为机体位置到涡环线最大与最小距离。

最终可以得到某点处无人机的x,y,z三向风速u,v,w:

\begin{matrix} \{\begin{array}{l} u = \frac{x - x_{M}}{r_{O}^{2}} \frac{\partial ψ}{\partial z} \\ v = \frac{y - y_{M}}{r_{O}^{2}} \frac{\partial ψ}{\partial z} \\ w = - \frac{1}{r_{O}} \frac{\partial ψ}{\partial r_{O}} \end{array} \end{matrix}

(3)

式中

r_{O}

为机体位置到涡环中心线的距离。

现对特殊位置的风速进行说明。

1)涡环中轴线处,即r_O=0时:由流线方程计算出的诱导速度趋近正无穷,不合理,因此该处速度由涡环位函数偏导计算,径向速度为0,轴向速度为^[9]:

\begin{matrix} w = \frac{Γ}{2 R} {(1 + {(\frac{z - z_{P}}{R})}^{2})}^{- 1.5} \end{matrix}

(4)

2)涡环线上,即r₀=r时:由式(3)可知,当距离为0时,诱导速度会解算至正无穷,不符合实际情况。故构造半径为r的封闭环形圆柱,引入诱导因子

ξ

,建立连续变化的涡核模型,其表达式为^[10]:

\begin{matrix} ξ = 1 - e x p (\frac{- r_{m i n}^{2}}{R^{2} (a t + b t^{2} + c t^{3})^{2}}) \end{matrix}

(5)

式中:t=2r/R;a,b,c为常数,a=0.42,b=0.08,c=-0.09。

修正后的风速为:

\begin{matrix} V_{w, c o r r} = ξ [\begin{array}{l} u \\ v \\ w \end{array}] \end{matrix}

(6)

1.1.2 多倾斜涡环对模型

实际情况下,微下击暴流风场往往由多个风暴中心(涡环)组成的,且水平辐射的外流也是非对称的,因此引入倾斜变换矩阵,通过多涡环叠加来模拟区域范围内的微下击暴流风场。

如图3所示,令主涡环坐标系与地面坐标系的夹角向量为

{(φ, θ, 0)}^{T}

,对应的旋转矩阵为

M (φ)

M (θ)

,则镜像涡环与地面系夹角向量为

{(- φ, - θ, 0)}^{T}

。通过矩阵变换

M (φ)

M (θ)

完成主涡环坐标系到地面坐标系的转换,同理可由矩阵变换

M (- φ)

M (- θ)

实现镜像涡环坐标系到地面坐标系的转换。其中:

\begin{matrix} M (φ) = [\begin{array}{l} c o s φ & 0 & s i n φ \\ 0 & 1 & 0 \\ - s i n φ & 0 & c o s φ \end{array}] \end{matrix}

(7)

\begin{matrix} M (θ) = [\begin{array}{l} 1 & 0 & 0 \\ 0 & c o s θ & - s i n θ \\ 0 & s i n θ & c o s θ \end{array}] \end{matrix}

(8)

图3 多倾斜涡环对设置示意图

Fig.3 Schematic diagram of the setup of multiple tilted vortex ring pairs

Full size|PPT slide

结合式(6),最终涡环地面坐标系下三维风矢量为:

\begin{matrix} \begin{matrix} V_{w, c o r r, o b l} = M (φ) M (θ) V_{w, c o r r, P} + M (- φ) M (- θ) V_{w, c o r r, I} \end{matrix} \end{matrix}

(9)

由

(x, y, z, R, v_{0}, r, φ, θ)

来确定唯一涡环模型,参照文献[11]和文献[12]的飞行仿真实验数据进行多涡环模型参数设置,各涡环模型参数见表1。

表1 各涡环模型参数表

Table 1 Parameter table of each vortex ring model

Parameter	Model name
Parameter	A	B	C	D
$x$ /m	1 700	1 700	800	2 800
$y$ /m	1 700	1 700	1 600	1 600
$z$ /m	610	610	400	400
$R$ /m	800	800	400	400
v₀/(m/s)	15	15	11	11
$r$ /m	500	500	200	200
$φ$ /(°)	0	15	0	15
$θ$ /(°)	0	30	0	15

图4~图8为各涡环模型在y=1500 m处剖面的平面风矢量分布图,模型A为对称涡环对,将模型A倾斜放置后得到模型B,另外增设尺度较小的对称涡环对模型C与倾斜涡环模型D,融合叠加后得到模型E。

图4 NASA 1988 年美国丹佛微下击暴流事故风场图^[12]

Fig.4 NASA's 1988 wind field map of the microburst accident in Denver, USA^[12]

Full size|PPT slide

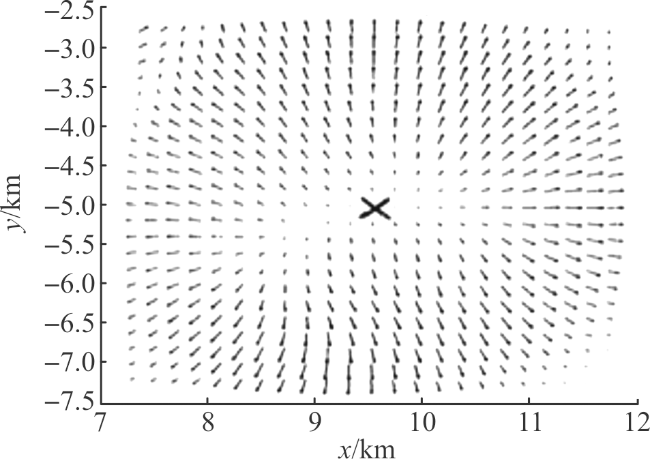
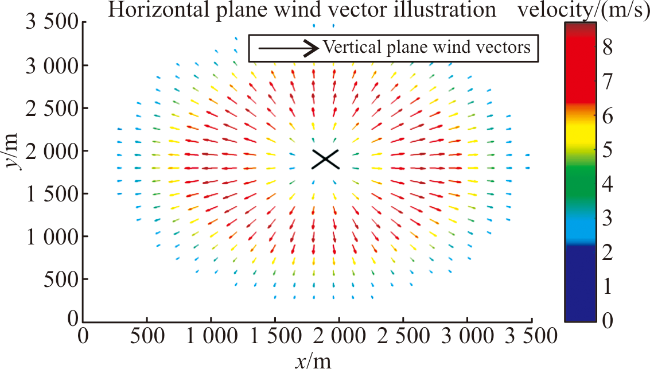
图5 单涡环对在z=100 m处剖面的风矢量分布图

Fig.5 Wind vector distribution diagram of the section at z=100 m for a single vortex ring pair

Full size|PPT slide

图6 模型A的风矢量分布图

Fig.6 Wind vector distribution diagram of model A

Full size|PPT slide

图7 模型B的风矢量分布图

Fig.7 Wind vector distribution diagram of model B

Full size|PPT slide

图8 模型E的风矢量分布图

Fig.8 Wind vector distribution diagram of model E

Full size|PPT slide

通过对比图4和图5实测风场数据的比较可以看出,对称涡环所构建的下击暴流风场有较高的对称性,与实际风场数据较为相似,但实际风场中仍存在部分非对称风速。

通过图6看出,涡环中心轴附近区域的风速垂直分量较大,且在水平方向,距离涡环中心轴越远风速越小,涡环外存在风速上卷,与实际下击暴流风场中近地面处风速变化几乎一致。

通过图6和8看出,在融合多涡环后,与单涡环对模型相比,垂直面内风矢量出现多处切变现象,且具有良好的三维特性,能够较为真实地反映微下击暴流的实际风速分布情况,模型空间特征合理,满足弹道仿真的要求。

1.2 Dryden大气紊流场模型

大气紊流是指大气中存在的不规则、混乱的气流运动,其形成与诸多因素有关,如风切变、热交换、地形诱导等,其基本特征是速度场沿空间和时间分布的不规则性,可以将速度场视为由均值与偏离量两部分组成,一般引入平稳性、正态性、冻结假设和各向同性假设,用随机过程的理论与方法进行描述^[8]。

Dryden模型与Von Karman模型是已被公认两种适用于飞行仿真的紊流模型,对于小型无人机而言,两种模型差别不大^[13],但Dryden模型频谱形式简单,有利于仿真计算,且小型无人机的姿态受风速梯度影响较小,故选取一维Dryden模型进行紊流场建模,通过时域法构建大气紊流场。

时域法构建大气紊流场是利用高斯白噪声,通过成形滤波器(大气紊流场模型通过空域、频域、时域变换即可得到)来实现,因此高斯白噪声、成形滤波器的质量决定了大气紊流场的质量^[14]。

1.2.1 白噪声优化

白化程度是衡量高斯白噪声优劣的重要指标,通过随机双交换法来改变高斯白噪声信号的内部顺序,降低信号间的相关程度,具体算法步骤如下^[15]:

1)随机选取一个白噪声序列

x_{i} (n)

其中,

i = 0, 1, 2, \dots; n = 0, 1, 2, \dots, N - 1

。当

i = 0

时,表示初始的自噪声序列。

2)将序列中任意两个点的数据

x_{i} (m)

x_{i} (l)

交换位置,得到新的噪声序列

x_{i + 1} (n)

。

3)计算新序列

x_{i + 1} (n)

的自相关函数

r_{i + 1}

。

\begin{matrix} r_{i + 1} = \frac{1}{N} \sum_{n = 0}^{N - k - 1} x_{i + 1} (n) x_{i + 1} (n + k) \end{matrix}

(10)

其中k=0,1,2,…,N-1。

4)计算自相关系数平方和S_i₊₁。

\begin{matrix} S_{i + 1} = \sum_{k = 1}^{N - 1} (r_{i + 1} {(k))}^{2} \end{matrix}

(11)

设

S_{0}

为原始序列

x_{0} (n)

的自相关系数平方和,以判断在步骤6)中

S_{1}

与

S_{0}

进行对比后循环次数是否

+ 1

;

5)当序列的自相关系数平方和小于设定的误差阈值,即

S_{i + 1} θ

或循环次数

i

达到最大循环次数

N_{m a x}

时,则停止交换,输出经过

x_{i + 1} (n)

;

6)若

S_{i + 1} S_{i}

,则

i = i + 1

,返回2);反之,返回1),重新执行上述步骤。

随机双交换方法仅改变了信号的内部分布,以减少相关性。功率谱密度(PSD)的均匀性是衡量噪声白化程度的一个重要指标^[14]。PSD分布越均匀,则噪声的随机性越强,质量越好。采用文献[16]的方法来生成白噪声,以一组长度为1 000的白噪声为例,设定阈值为10,最大循环次数为10 000,计算随机双交换前后白噪声序列的功率谱密度,结果如图9所示。

图9 优化后功率谱密度(PSD)对比图

Fig.9 Comparison chart of power spectral density (PSD) after optimization

Full size|PPT slide

通过图9与图10可看出,优化后白噪声序列的PSD分布更加均匀,自相关系数平方和随交换次数降低。

图10 自相关系数平方和变化图

Fig.10 Change graph of sum of squares of autocorrelation coefficient

Full size|PPT slide

1.2.2 成形滤波器

根据Dryden模型,由时间频谱函数得到三向速度及对应的相关函数:

\begin{matrix} \{\begin{array}{l} Φ_{u u} (ω) = σ_{u}^{2} \frac{L_{u}}{π V} \frac{1}{1 + ((L_{u} {/ V) ω)}^{2}} \\ Φ_{v v} (ω) = σ_{v}^{2} \frac{L_{v}}{π V} \frac{1 + 12 ((L_{v} {/ V) ω)}^{2}}{((1 + 4 (L_{v} {/ V) ω)}^{2})^{2}} \\ Φ_{w w} (ω) = σ_{w}^{2} \frac{L_{w}}{π V} \frac{1 + 12 ((L_{w} {/ V) ω)}^{2}}{((1 + 4 (L_{w} {/ V) ω)}^{2})^{2}} \end{array} \end{matrix}

(12)

\begin{matrix} \{\begin{array}{l} R_{u u} (τ) = σ_{u}^{2} e x p (- \frac{V}{L_{u}} |τ|) \\ R_{v v} (τ) = σ_{v}^{2} (1 - \frac{V}{4 L_{v}} |τ|) e x p (\frac{V}{2 L_{v}} |τ|) \\ R_{w w} (τ) = σ_{w}^{2} (1 - \frac{V}{4 L_{w}} |τ|) e x p (- \frac{V}{2 L_{w}} |τ|) \end{array} \end{matrix}

(13)

式中:

σ_{u}, σ_{v}, σ_{w}

为三向紊流强度,根据飞行高度与经验^[14],

σ_{u} = σ_{v} = σ_{w}

,取1.2 m/s;对于各同向性紊流,

L_{u}, 2 L_{v}, 2 L_{w}

为三向紊流尺度,

L_{u} = 2 L_{v} = 2 L_{w}

,取200 m^[14];

V

为无人机速度,取60 m/s。最终设计成形滤波器进行输出,具体如下。

在控制过程中,成形滤波器能够将白噪声转化成有色噪声。白噪声的频谱为常值,令它为单位值,单位强度的白噪声

r (t)

通过一个传递函数为

G (s)

的滤波器,产生随机过程

u (t)

,则

u (t)

的频谱函数为:

\begin{matrix} Φ (ω) = G^{*} (i ω) G (i ω) = {|G (i ω)|}^{2} \end{matrix}

(14)

式中G^*表示G的复共轭。将紊流的各项时间频谱函数按上式进行分解,得到产生给定频谱所需的成形滤波器的传递函数

G (s)

\begin{matrix} \{\begin{array}{l} G_{u} (s) = \frac{K_{u}}{T_{u} s + 1} \\ K_{u} = σ_{u} \sqrt{\frac{L_{u}}{π V}} \\ T_{u} = \frac{L_{u}}{V} \\ G_{v} (s) \approx \frac{K_{v}}{T_{v} s + 1} \\ K_{v} = σ_{u} \sqrt{\frac{L_{u}}{π V}} \\ T_{v} = \frac{2}{\sqrt{3}} \frac{L_{v}}{V} \\ G_{w} (s) \approx \frac{K_{w}}{T_{w} s + 1} \\ K_{w} = σ_{w} \sqrt{\frac{L_{w}}{π V}} \\ T_{w} = \frac{2}{\sqrt{3}} \frac{L_{w}}{V} \end{array} \end{matrix}

(15)

为方便实现,将

G_{v}

G_{w}

简化为一阶环节,各环节的输入是均值为0,方差为1的近似Gauss分布的白噪声,故还须对滤波器进行离散化。

引入修正系数k_P和k_Q可得^[17]:

\begin{matrix} \{\begin{array}{l} x_{i + 1} = k_{P} P x_{i} + k_{Q} Q r_{i + 1} \\ P = e^{- h / T} \\ Q = σ_{x} \sqrt{e^{- 2 h / T}} \end{array} \end{matrix}

(16)

式中:x_i为离散序列x第i点的值;h为采样周期。

经过仿真计算,得到三向紊流速度、风速相关性对比如图11、图12所示。

图11 v,u,w三向紊流风速图

Fig.11 v,u,w three-way turbulent wind speed diagram

Full size|PPT slide

图12 横纵向风速相关性检验

Fig.12 Horizontal and longitudinal wind speed correlation test

Full size|PPT slide

通过图12可知,仿真结果与理论值比较接近,具有较高吻合度,针对文中研究的固定翼无人机,可在一定程度上反映出其在大气环境中的扰动特性。

1.3 风场融合

考虑风场主要特征与风矢量的变化性,将紊流场融入至微下击暴流场模型E中,得到复合下击暴流风场模型,记为模型F,具体融合过程如图13所示。

图13 融合过程示意图

Fig.13 Schematic diagram of the fusion process

Full size|PPT slide

假设无人机从复合下击暴流风场竖向对称面中穿过,不受风场影响,保持高度在1 050 m,可得到图14中实线部分风速,可以看出,模型F规避了部分风速线性化,且可较好描述多因素耦合复杂情况下的大气流动。

图14 融合前后的风场对比图

Fig.14 Wind field comparison before and after fusion

Full size|PPT slide

2 计及风场的平飞段弹道模型

在风场作用下,一般是将风的作用引入至飞行器速度的变化中,以地速为标准,将风的影响归结为附加攻角、侧滑角的变化。无人机空间六自由度运动方程采用苏式坐标系建立,具体参考文献[18-19]。当风矢量发生变化时,无人机空速的变化可视为存在偏差的标准空速,弹道倾角、弹道偏角随之变化,引起攻角、侧滑角与速度倾斜角的变化,进一步影响空气动力与力矩,为实现定高巡航,控制系统做出相应调整以抵消风矢量的影响。

巡航段平飞状态下由于气动状态相对稳定,工程设计中一般使用PID控制器对其进行控制,设计高度、俯仰、姿态控制回路,保证巡航段稳定的飞行高度;设计滚转姿态及侧向位置控制回路,保证航线平面稳定跟踪;设计空速闭环控制回路,调整电机输出,实现空速的稳定跟踪。

3 弹道仿真分析

3.1 仿真条件

以电动无人机为对象进行仿真计算,其发射初始条件如表2所示,仿真状态视为依次经过抛撒或分离、降高转平后理想的飞行状态。

表2 飞行状态初值表

Table 2 Flight status initial value table

Parameter	Value
(x,y,z)/m	(0,1 000,1 700)
(V_x,V_y,V_z)/(m/s)	(60,0,0)
$(ϑ, ψ, γ)$ /(°)	(0,0,0)
(ω_x,ω_y,ω_z)/(rad/s)	(0,0,0)

3.2 不同风场强度下的弹道仿真

将无风状态下记为状态1。由风切变定义知,风速大小是风切变强度的决定因素,通过对比JAWS的多普勒雷达测量统计结果和美军飞行数据记录器FDR提取的微下击暴流风切变数据比较^[20],确定复合微下击暴流模型的中心诱导风速分别为10 m/s,15 m/s,20 m/s,25 m/s,依次记为状态2~状态5。

以平飞时间200 s为仿真截止条件,模拟无人机穿越复合微下击暴流风场飞行,各飞行状态采用同一的控制策略与参数,以状态1仿真结果为基准进行对照分析。表3为各状态下飞行参数的仿真结果,k为能量消耗相对变化率,d为掉高高度。

表3 飞行参数仿真结果

Table 3 Flight parameter simulation results table

Condition	x/m	K/%	d/m
1	12 000	—	0
2	11 872	-5.14	168.72
3	11 826	-3.34	298.62
4	11 784	-1.80	446.59
5	11 790	-2.46	537.02

由表3和图15、图16可以看出,无风状态下,无人机经过短暂爬升后,可以按照预设航线进行平飞,受到复合微下击暴流场的影响,无人机巡航段弹道特征发生较大变化:1)巡航高度随着中心诱导速度的增大出现掉高现象,尤其是在状态5中掉高达到537 m,若同等风场条件下,掉高高度大于飞行高度,则极易造成坠毁风险,相较于侧向位置偏差,这类风险在各类试验测试中是最重要的;2)受北向风影响,状态2消耗能量最低,状态3~状态5由于存在掉高需要爬升故北向距离相对减小、消耗相对增大,在非严苛的环境下动力余量尚足以保证飞行任务,也可通过调整航线对风场加以利用,进而减小能量消耗;3)侧向位置与复合风场中心诱导速度的大小呈正相关,由于无人机是从风场竖向对称面中穿越飞行,初始受到的横向风较小,滚转通道快速稳定后再受到较为连续的横向风后,控制系统可以对风速变化带来的影响进行及时控制,但模型建立精细度不足,状态5在40 s左右的跳变在实际飞行中很难执行,横向操纵性较低的无人机极易发散失控。

图15 高度变化对比图

Fig.15 Comparison chart of height

Full size|PPT slide

图16 侧向位置变化对比图

Fig.16 Comparison chart of lateral position changes

Full size|PPT slide

图17~图19依次为地面坐标系下北、天、东三向风速在飞行时间60 s内的变化。可以看出各向风速变化较为连续,随着诱导速度增大,风速并非成比例变化,受紊流叠加的影响,风速变化更具随机性;受复合微下击暴流场的三维性影响,状态4、状态5在35 s左右开始天向、东向速度基本接近。

图17 北向风速对比图

Fig.17 Comparison chart of northward wind speed changes

Full size|PPT slide

图18 天向风速对比图

Fig.18 Comparison chart of skyward wind speed changes

Full size|PPT slide

图19 东向风速对比图

Fig.19 Comparison chart of east wind speed changes

Full size|PPT slide

通过图20、图21可以看出,紊流对攻角、侧滑角影响明显,出现多处波动,可以说明小型无人机气动特性敏感,状态2~状态4下攻角、侧滑角持续保持在一个相对稳定的范围内;受到了3个微下击暴流涡环中心垂直气流的影响,攻角出现了多个峰值;无人机在飞出子涡环区域后会出现攻角突增、侧滑角振幅增大,故抗微下击暴流的姿态控制能力应置于边缘风场区域进行考量;受到控制系统影响,状态2~状态4间攻角、侧滑角变化较为相似,但随诱导速度增大状态5下攻角、侧滑角波动显著增大,基本处于控制边界。

图20 攻角变化对比图

Fig.20 Comparison chart of changes in attack angle

Full size|PPT slide

图21 侧滑角变化对比图

Fig.21 Comparison chart of changes in sideship angle

Full size|PPT slide

4 结论

由建立优化后的紊流场与下击暴流场,将两者融合后得到复合微下击暴流场,通过仿真计算,得到以下结论:1)所建立的复合风场具有较高的真实性与三维特性,可弥补无人机设计工程中对风场描述的不足,并应用于性能分析、设计优化、事故复现等;2)复合微下击暴流场的中心诱导速度对飞行高度有较大影响,无人机在穿越强度高的下击暴流场或遭受地形引起的风切变时,极易造成掉高坠毁事故。

文中尚未研究空中布撒无人机在抛撒段以及自杀式无人机在末制导段受复合微下击暴流场的影响。受限于控制系统性能与各子系统的设计余量,各类无人机在微下击暴流场下的飞行性能需要独立分析,下一步研究将着重于基于现有设计,通过改进控制算法提高无人机的抗风能力。

参考文献

列表( 原文顺序 | 文献年度倒序 | 文中引用次数倒序 ) 可视化分析

[1]	郭锡福. 远程火炮武器系统射击精度分析[M]. 北京: 国防工业出版社, 2004. GUO X F. Analysis of shooting accuracy of long-range artillery weapon systems[M]. Beijing: National Defense Industry Press, 2004. 本文引用 [1]

[2]	李宏海, 欧进萍. 我国下击暴流的时空分布特性[J]. 自然灾害学报, 2015, 24(6):9-18. LI H H, OU J P. Spatial and temporal distribution characteristics of downbursts in China[J]. Journal of Natural Disasters, 2015, 24(6): 9-18. 本文引用 [1]

[3]

陈健伟, 王良明, 傅健. 用于实时弹道仿真的低空风切变复合模型[J]. 系统工程与电子技术, 2019, 41(11):2597-2604.

https://doi.org/10.3969/j.issn.1001-506X.2019.11.24

摘要

风切变是一种形成概率高、危害范围广的气象现象,对弹箭飞行具有较大影响。针对几种典型低空风切变的流动特点,基于位势流动理论,分别建立了微下击暴流涡环模型、过山气流圆柱绕流模型和低空急流平面壁面射流模型。在此基础上,以发射坐标系为基准,提出一种考虑天气和地形的低空风切变复合模型。以某122 mm火箭弹为例,进行算例仿真。仿真结果表明:所建立的低空风切变复合模型具有良好的三维特性,能够合理描述典型风切变现象的气体流动特点。应用于实时弹道仿真中,可有效反映出复杂环境下不同种类低空风切变对弹箭飞行的影响规律。

CHEN

J W

, WANG

L M

, FU

. A low-altitude wind shear composite model for real-time ballistic simulation[J]. Systems Engineering and Electronics, 2019, 41(11):2597-2604.

本文引用 [1]

[4]	陈健伟, 王良明, 李子杰. 两种典型低空风切变对火箭弹弹道特性的影响[J]. 北京航空航天大学学报, 2018, 44(5):1008-1017. CHEN J W, WANG L M, LI Z J. The impact of two typical low-altitude wind shears on the ballistic characteristics of rockets[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(5):1008-1017. 本文引用 [1]

[5]

王晋, 田军委, 刘雪松, 等. 湿微下击暴流对火炮外弹道精度影响分析[J]. 弹箭与制导学报, 2022, 42(6):99-106.

https://doi.org/10.15892/j.cnki.djzdxb.2022.06.015

摘要

针对湿微下击暴流特性会对火炮射程、侧偏等参数产生一定的偏差,对火炮的射击精度影响较大问题,以155 mm火炮杀爆弹为研究对象,基于涡环原理与流体力学建立微下击暴流与雨滴运动模型,并融合为适用于弹道分析计算的湿微下击暴流模型,将湿微下击暴流模型与火炮6自由度弹道方程结合,仿真并分析不同初始涡环中心诱导速度对火炮平射与曲射两种发射方式射击精度的影响。实验结果表明:对于低伸弹道,外弹道侧偏与偏航角增加比例随着初始中心涡环诱导速度的增加而减小;而对于远距离射击,火炮射程随着初始涡环中心诱导速度的增大而减小,严重影响火炮的射击精度与杀伤效果。

WANG

, TIAN

J W

, LIU

X S

, et al. Analysis of the impact of wet microbursts on the external ballistic accuracy of artillery[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2022, 42(6):99-106.

本文引用 [1]

[6]	王晋, 田军委, 刘雪松, 等. 山地低空气流对火炮外弹道产生偏差分析[J]. 火力与指挥控制, 2023, 48(8):53-59. WANG J, TIAN J W, LIU X S, et al. Analysis of deviations in external ballistics caused by mountain low-altitude airflows[J]. Fire Control and Command Control, 2023, 48(8):53-59. 本文引用 [1]

[7]	刘时杰, 徐浩军, 薛源, 等. 具有湍流效应的不规则微下击暴流构建方法研究[J]. 飞行力学, 2014(4):303-307. LIU S J, XU H J, XUE Y, et al. Study on the construction method of irregular microburst with turbulence effects[J]. Flight Dynamics, 2014(4): 303-307. 本文引用 [1]

[8]	肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993. XIAO Y L, JIN C J. Principles of flight in atmospheric disturbances[M]. Beijing: National Defense Industry Press, 1993. 本文引用 [2]

[9]

马泽昊, 郭利明, 张泽华, 等. 基于涡环法的微下击暴流风场建模分析与应用[C]// 第八届中国航空学会青年科技论坛论文集. 广东: 中国航空学会, 2018:701-710.

Z H

, GUO

L M

, ZHANG

Z H

, et al. Modeling and application of microburst wind field based on vortex ring method[C]// Proceedings of the 8th Youth Science and Technology Forum of the Chinese Society of Aeronautics and Astronautics. Chinese Society of Aeronautics and Astronautics, Guangdong: CSA, 2018:701-710.

本文引用 [1]

[10]	陶杨, 韩维, 吴亮. 虚拟时变微下击暴流的数值仿真方法[J]. 应用力学学报, 2014, 31(6):847-852. TAO Y, HAN W, WU L, et al. Numerical simulation method of virtual time-varying microburst[J]. Chinese Journal of Applied Mechanics, 2014, 31(6):847-852. 本文引用 [1]

[11]	高振兴. 复杂大气扰动下大型飞机飞行实时仿真建模研究[D]. 南京: 南京航空航天大学, 2009. GAO Z X. Research on real-time simulation modeling of large aircraft flight under complex atmospheric disturbances[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. 本文引用 [1]

[12]	WANKE C R, HANSMAN R J. A data fusion algorithm for multi-sensor microburst hazard assessment[C]// AIAA Atomospheric Flight Mechanics Conference. Reston:AIAA, 1992:17-29. 本文引用 [3]

[13]	王文龙. 大气风场模型研究及应用[D]. 长沙: 国防科学技术大学, 2009. WANG W L. Research and application of atmospheric wind field models[D]. Changsha: National University of Defense Technology, 2009. 本文引用 [1]

[14]	李传荣, 唐伶俐, 李晓辉, 等. 无人机遥感载荷成像风场传递效应分析[M]. 北京: 科学出版社, 2018. LI C R, TANG LL, LI X H, et al. Effect of wind field transmission on UAV remote sensing payload imaging[M]. Beijing: Science Press, 2018. 本文引用 [4]

[15]	JACQUEMOD G, ODET C, GOUTTE R. Image resolution enhancement using subpixel camera displacement[J]. Signal Processing, 1992, 26(1): 139-146. 本文引用 [1]

[16]	蔡坤宝, 罗汉文. 产生高斯随机序列的新方法[J]. 上海交通大学学报, 2004, 38(12):2052-2056. CAI K B, LUO H W, et al. A new method for generating Gaussian random sequences[J]. Journal of Shanghai Jiao Tong University, 2004, 38(12):2052-2056. 本文引用 [1]

[17]	屈香菊, 李勇. 一种改进的紊流风模型及其仿真算法[J]. 系统仿真学报, 2004, 16(1):10-16. QU X J, LI Y. An improved turbulence wind model and its simulation algorithm[J]. Journal of System Simulation, 2004, 16(1):10-16. 本文引用 [1]

[18]	钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2013. QIAN X F, LIN R X, ZHAO Y N. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2013. 本文引用 [1]

[19]	林海, 王晓芳. 飞行力学数值仿真[M]. 北京: 北京理工大学出版社, 2018. LIN H, WANG X F, et al. Numerical simulation of flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2018. 本文引用 [1]

[20]	高振兴, 顾宏斌. 用于飞行实时仿真的微下击暴流建模研究[J]. 系统仿真学报, 2008, 20(23):6524-6528. GAO Z X, GU H B. Microburst modeling for real-time flight simulation[J]. Journal of System Simulation, 2008, 20(23):6524-6528. 本文引用 [1]

PDF(5453 KB)

106

Accesses

Citation

Detail

段落导航

摘要
Abstract
关键词
Key words
引用本文
0 引言
1 复合微下击暴流风场模型的建立
1.1 多倾斜涡环对风切变模型
图1 下击暴流形成示意图
1.1.1 对称涡环模型
图2 对称涡环对设置示意图
1.1.2 多倾斜涡环对模型
图3 多倾斜涡环对设置示意图
表1 各涡环模型参数表
图4 NASA 1988 年美国丹佛微下击暴流事故风场图[12]
图5 单涡环对在z=100 m处剖面的风矢量分布图
图6 模型A的风矢量分布图
图7 模型B的风矢量分布图
图8 模型E的风矢量分布图
1.2 Dryden大气紊流场模型
1.2.1 白噪声优化
图9 优化后功率谱密度(PSD)对比图
图10 自相关系数平方和变化图
1.2.2 成形滤波器
图11 v,u,w三向紊流风速图
图12 横纵向风速相关性检验
1.3 风场融合
图13 融合过程示意图
图14 融合前后的风场对比图
2 计及风场的平飞段弹道模型
3 弹道仿真分析
3.1 仿真条件
表2 飞行状态初值表
3.2 不同风场强度下的弹道仿真
表3 飞行参数仿真结果
图15 高度变化对比图
图16 侧向位置变化对比图
图17 北向风速对比图
图18 天向风速对比图
图19 东向风速对比图
图20 攻角变化对比图
图21 侧滑角变化对比图
4 结论
参考文献

收稿日期	出版日期
2024-08-19	2025-03-12
发布日期
2025-03-12

模态框（Modal）标题

选择文件类型/文献管理软件名称

选择包含的内容

摘要

Abstract

关键词

Key words

引用本文

0 引言

1 复合微下击暴流风场模型的建立

1.1 多倾斜涡环对风切变模型

图1 下击暴流形成示意图

1.1.1 对称涡环模型

图2 对称涡环对设置示意图

1.1.2 多倾斜涡环对模型

图3 多倾斜涡环对设置示意图

表1 各涡环模型参数表

图4 NASA 1988 年美国丹佛微下击暴流事故风场图[12]

图5 单涡环对在z=100 m处剖面的风矢量分布图

图6 模型A的风矢量分布图

图7 模型B的风矢量分布图

图8 模型E的风矢量分布图

1.2 Dryden大气紊流场模型

1.2.1 白噪声优化

图9 优化后功率谱密度(PSD)对比图

图10 自相关系数平方和变化图

1.2.2 成形滤波器

图11 v,u,w三向紊流风速图

图12 横纵向风速相关性检验

1.3 风场融合

图13 融合过程示意图

图14 融合前后的风场对比图

2 计及风场的平飞段弹道模型

3 弹道仿真分析

3.1 仿真条件

表2 飞行状态初值表

3.2 不同风场强度下的弹道仿真

表3 飞行参数仿真结果

图15 高度变化对比图

图16 侧向位置变化对比图

图17 北向风速对比图

图18 天向风速对比图

图19 东向风速对比图

图20 攻角变化对比图

图21 侧滑角变化对比图

4 结论

{{custom_sec.title}}

{{custom_sec.title}}

参考文献

{{custom_fnGroup.title_cn}}

脚注

图4 NASA 1988 年美国丹佛微下击暴流事故风场图^[12]