基于火箭橇的变马赫气流扩张通道研究

谢波涛, 刘振, 张晨辉, 刘显为

弹箭与制导学报 ›› 2024, Vol. 44 ›› Issue (2) : 82-89.

PDF(5392 KB)
中文  |  English
文章检索
高级检索
弹箭与制导学报
PDF(5392 KB)
弹箭与制导学报 ›› 2024, Vol. 44 ›› Issue (2) : 82-89. DOI: 10.15892/j.cnki.djzdxb.2024.02.013

基于火箭橇的变马赫气流扩张通道研究

作者信息 +

Research on Variable Hetz Airflow Expansion Channel Based on Rocket Sled

Author information +
文章历史 +

摘要

针对火箭橇气流通道装置开展设计与数值模拟研究。首先,将气流扩张通道内部划分为初始源流膨胀区、消波区和均匀流试验区,然后,应用Foelsch方法对初始膨胀段型线进行设计,采用基于轴线马赫数预设的特征线方法对过渡消波段进行设计,最后,针对扩张比为2.5的火箭橇气流扩张装置,在运行速度为1.5Ma、2Ma、2.5Ma和3Ma条件下开展数值模拟分析,结果表明,通道进口膨胀波随着运行速度的增加而减弱,1.5Ma速度条件下的相对压力峰值为0.14 MPa,3Ma速度条件的相对压力峰值为0.018 MPa,相对压力峰值下降约87%,使进口条件得到改善,最大马赫数模拟偏差为3.9%,静压模拟偏差为6.5%。

Abstract

The application of airflow expansion channel device in rocket sled test can obtain higher airflow velocity at the exit, so as to realize the simulation of hypersonic environment. The design and numerical simulation of airflow channel device for rocket sled are studied. Firstly, the internal part of the air expansion channel is divided into initial source flow expansion area, wave attenuation area and uniform flow test area. Foelsch method is used to design the initial expansion section profile, and the characteristic method based on the preset Mach number of the axis is used to design the transition wave attenuation band. On this basis, numerical simulation analysis is carried out for the rocket sled air expander with a growth rate of 2.5 at the operating speeds of 1.5Ma, 2Ma, 2.5Ma and 3Ma. The results showed that the expansion wave at the inlet of the channel weakened with the increase of the operating speed. The peak relative pressure at 1.5Ma is 0.14MPa, and the peak relative pressure at 3Ma is 0.018 MPa. The decrease of relative pressure is about 87% and the inlet condition is improved. After data comparison,the maximum mach number simulation deviation is 3.9%, and the static pressure simulation deviation is 6.5%.

关键词

火箭橇 / 高超声速环境 / 气流扩张通道 / 特征线方法

Key words

rocket sled / hypersonic environment / air-expansion channel / characteristic method

引用本文

EndNote

Ris (Procite)

Bibtex

导出引用
谢波涛, 刘振, 张晨辉, 等. 基于火箭橇的变马赫气流扩张通道研究[J]. 弹箭与制导学报, 2024, 44(2): 82-89 https://doi.org/10.15892/j.cnki.djzdxb.2024.02.013
XIE Botao, LIU Zhen, ZHANG Chenhui, et al. Research on Variable Hetz Airflow Expansion Channel Based on Rocket Sled[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2024, 44(2): 82-89 https://doi.org/10.15892/j.cnki.djzdxb.2024.02.013
中图分类号： TJ76 (导弹)   

0 引言

火箭橇试验系统以火箭发动机为动力,沿高精度轨道高速运行,实现在地面模拟被试品高空真实超高声速条件的目的。人们针对各类型火箭橇试验,开展了广泛的研究。肖军等[1]利用火箭橇全弹道参数,对常规兵器火箭橇试验时橇车速度影响因素进行了分析。夏有财等[2]在分析火箭橇运动计算方法的基础上,对常规动力学算法进行优化,引入了能量耗散阻力参数,使运动误差计算结果减小到0.11%。余元元等[3]采用数值方法研究了火箭橇轨道系统的瞬态动力学特性。
目前的火箭橇结构主要是将被试品直接装载加速,在单个发动机推力难以提升的条件下,为了获得更高的速度,只能增加发动机的数量。而随着整体系统推重比的下降,火箭橇试验的速度逼近极限。为了在现有条件下实现更高速度的模拟,人们提出在橇体结构上安装气流扩张装置,利用气流在扩张通道中的增速效应,使被试品获得高于橇体运行速度的高超声速条件。汪运鹏等[4]针对二维轴对称型面的气流喷管设计,归纳了传统高超声速喷管设计的主要理论和常用方法。刘亚洲等[5]采用特征线法,对等逆压梯度分布的喷管延伸段型面开展了设计,并进行了仿真校验。Zhou等[6]通过设计定马赫喷管火箭橇,实现对海拔13~15 km、速度2.4Ma高空环境的模拟。王英鹏、陈以勒等[7-8]提出了喷管型面优化方法。
为进一步提升火箭橇试验被试品的气流模拟速度与海拔,人们对火箭橇气流扩张通道装置开展设计与数值模拟研究。Foelsch等[9]应用Foelsch方法对初始膨胀段型线进行设计。Sivells等[10]采用基于轴线马赫数预设的特征线方法对过渡消波段进行设计,并通过火箭橇试验对气流装置的设计结果进行分析验证。

1 气流扩张通道的设计方法

火箭橇超声速环境模拟试验是利用橇载气流扩张装置,使经过的气流获得比实际物理运行过程更高的速度,火箭橇超声速气动环境模拟装置的典型结构如图1所示。
图1 火箭橇超声速气动环境模拟装置结构示意图

Fig.1 Structural schematic diagram of rocket sled supersonic aerodynamic environment simulation device

Full size|PPT slide

该产品橇结构中,被试品放置在气流扩张通道的后部。当火箭橇以超声速运行时,气流在扩张通道内进一步膨胀加速,从而使通道尾部的被试品获得更高的环境模拟速度。
变马赫火箭橇试验中,在特定速度下启动释放装置,气流扩张装置由固定状态变为自由状态,在气动力作用下绕转轴向内侧旋转,改变了扩张比(出口与入口的面积比),可在相同火箭橇运行速度下,获得更高速度的试验环境,从而实现变马赫的目的。
火箭橇气流扩张通道装置可以分为初始源流膨胀区、消波区和均匀流试验区,扩张通道装置的结构示意图如图2所示。图中,Ⅰ区为初始源流膨胀区;Ⅱ区为消波区;Ⅲ区为均匀流试验区。理论分析表明,气流在经过喉部位置后,在I区内为点源流动,该区域内所有点的速度方向均与O点呈径向流动。在经过BD线进入Ⅱ区后,加速膨胀的气流开始转变流动角度,逐渐过渡为平行于x轴方向的流动。最后在跨过特征线CE进入Ⅲ区后,气流达到设计扩张速度,方向为均匀轴向流动。
图2 扩张通道装置结构示意图

Fig.2 Schematic diagram of expansion channel device

Full size|PPT slide

通过对扩张通道内部的结构分析,可以将通道的型线分为AB初始膨胀段、BC过渡消波段以及C点以后的均匀试验段。实际上,当气流在均匀试验段时,气流表现为轴向流动,因此该段曲线为直线段。下面主要讨论AB初始膨胀段、BC过渡消波段的设计方法。

1.1 初始膨胀段设计方法

气流在Ⅰ区可以假设为均匀源流,因此在初始膨胀段起始位置A处有:
y=y*dydxx=0=0
(1)
式中y*表示进口处喷管的宽度。而在初始膨胀段尾部B处有:
y=rBsinβBdydxx=xB=tanβBddxdydxx=xB=0
(2)
式中:rB为源流半径;βB为B点处气流的方向角度;xB为B点的横坐标。应用Foelsch方法可以获得满足边界约束式(1)和式(2)的曲线,即
y=y*+ tan βBxBx2 1-x3xB
(3)
而xB的表达式为:
xB= 32(yB-y*)cot β B
(4)
实际工程应用中,B处的气流角度一般选择为进口气流普朗特-迈耶角度的一半,即
βB= 12v(Ma)
(5)
式中v(Ma)为气流的普朗特-迈耶函数,其表达式为:
v= γ+1γ-1arctan γ+1γ-1(Ma2-1)-arctan(Ma2-1)
(6)
式中γ为气体的比热比常数。

1.2 过渡消波段设计方法

在完成初始源流膨胀段AB曲线的设计后,可以根据源流假设得到消波区边界BD线上的流动参数,结合给定DE段轴向马赫数的分布,通过求解特征线方程确定消波区BC段曲线位置。
超声速流动控制方程属于双曲型方程,因而存在特征线。对于定常无旋的二维流动,特征线方程和相容性方程可以表示为:
(Ma2-1)1/21+(γ-1)Ma2dMaMa±dθ=0
(7)
dydx=tan θ∓arcsin1Ma
(8)
式中θ为气流方向角,其表达式为:
θ=arctan vyvx
(9)
轴线DE上的马赫数分布可以应用五点四次贝塞尔曲线[11]给出,如图3所示为应用四次贝塞尔曲线的轴向马赫数示意图。
图3 轴向马赫数示意图

Fig.3 Axial Mach number plot

Full size|PPT slide

图3中横坐标表示轴向长度,纵坐标表示轴向马赫数的分布。从图中可以看到,当P1~P5五个控制点位置给定后,就能够通过控制多边形建立对应的函数关系。贝塞尔曲线的关系式为:
p(t)=[t4 t3 t2 t 1]· 1-46-41-412-12406-12600-4400010000P1P2P3P4P5
(10)
消波区Ⅱ区与均匀流试验区Ⅲ区的分界EC线可以认为是E点发出的左行马赫线CL,并且EC上所有流动参数保持不变,根据轴线上马赫数的分布有:
MaEC=MaEθEC=0
(11)
式中MaE表示E点处的马赫数。据此可以根据质量守恒关系,确定C点的坐标。
建立BD,DE,EC型线上的流动参数后,利用特征线迭代求解方法就可以求解消波区Ⅱ区内的流动参数。图4为特征线迭代求解示意图。
图4 特征线方程迭代求解示意图

Fig.4 Schematic diagram of iterative solution for characteristic line equation

Full size|PPT slide

图4中BD线上的参数可以利用源流理论求解得到,而轴线上的参数则是通过给定分布建立,因此利用1点处的左行特征线CL和2点处的右行特征线CR获得3点处的坐标位置,依次迭代求解可获得沿着轴线方向上的特征线。最后利用质量守恒原理,获得喷管壁面型线坐标。图5为特征线方法的设计结果。
图5 特征线方法设计结果

Fig.5 Design results of feature line method

Full size|PPT slide

2 流场数值模拟分析

2.1 结构模型与网格划分

应用上述气流扩张通道设计方法,得到的通道壁面二维设计结果如图6所示。横坐标表示橇体运行的轴线方向,纵坐标表示扩张通道的宽度,yi表示进口位置的宽度。
图6 气流扩张通道二维设计结果

Fig.6 Two dimensional design results of airflow expansion channel

Full size|PPT slide

双轨火箭橇设计气流扩张通道结构如图7所示。该气流扩张通道由顶架、底架和内表面构成,通道出口布置有被试品和支撑架。其中,橇体长度为3 700 mm,气流通道的长度、高度分别为2 800 mm和1 000 mm,宽度为1 080 mm,被试品为底面直径260 mm、高480 mm的圆锥体,位于气流通道的正中间,锥头与入口距离为2 500 mm。
图7 双轨火箭橇气流通道结构

Fig.7 Dual track rocket sled airflow channel structure

Full size|PPT slide

由于流场对称性,选取半流场进行分析,图8为气流扩张通道火箭橇流场仿真区域。图8中橇体长度为l,选取前部流场长度为8l,后部流场长度为5l,环境半径为10l。对上述结构进行网格划分,得到的结果如图9所示。
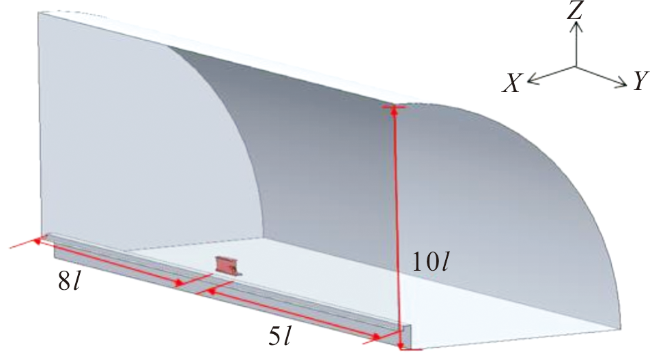
图8 气流扩张通道火箭橇流场仿真区域

Fig.8 Simulation area of rocket sled flow field in airflow expansion channel

Full size|PPT slide

图9 气流扩张通道火箭橇网格划分结果

Fig.9 Grid division results of rocket sled in airflow expansion channel

Full size|PPT slide

从图8、图9中可以看出,所生成的橇体表面网格贴合性好,共划分网格单元数为8 871 791,生成网格节点数为3 325 358。

2.2 数值模拟结果分析

采用SST k-ω湍流模型[12]分别对橇体运行速度1.5Ma、2Ma、2.5Ma和3Ma四种状态进行数值模拟分析,进口给定静压与速度,出口为超音速边界条件,流场外表面给定远场边界条件,橇体及地面给定壁面边界条件,对称面给定对称边界条件。为便于观察,在气流通道结构顶架和底架的对称面上建立参考平面,得到该平面上气流马赫数分布结果如图10所示。
图10 不同运行速度条件下气流扩张通道内部马赫数分布

Fig.10 Mach number distribution inside airflow expansion channels under different operating speed conditions

Full size|PPT slide

从图10中可以看出,超声速气流在进入扩张通道后,由于膨胀作用,在轴线方向上不断加速,到达出口被试品处速度达到最大,之后进入大气自由膨胀,速度逐渐下降。随着橇体运行速度的不同,气流内通道内部的加速过程也不同。当橇体运行速度较低时,气流通道内部的加速过程缓慢,出口速度变化不大,而随着橇体运行速度的增大,气流通道的加速过程急速上升,并在出口达到满足设计要求的气流速度。图11为沿轴线提取气流通道内部的马赫数变化情况。其中横坐标表示轴线方向长度,纵坐标表示马赫数。
图11 不同运行速度下气流通道内部轴线上马赫数分布

Fig.11 Mach number distribution on the internal axis of airflow channels at different operating speeds

Full size|PPT slide

从图11中可以看出,气流在进入气流通道时,由于进口壁面作用会形成膨胀波,从而导致气流速度的下降。在扩张通道的作用下,气流会逐渐加速,最终在出口达到满足要求的更高速度。图12为4种运行速度下气流通道内部的压力分布结果。
图12 不同运行速度条件下气流扩张通道内部压力分布

Fig.12 Pressure distribution inside the airflow expansion channel under different operating speed conditions

Full size|PPT slide

从图12中可以看出,超声速气流在进口位置由于受到壁面作用的影响,会形成一道膨胀波,导致进口压力升高,速度下降。膨胀波的强度随着运行速度的增大而减小,对进口气流的减速作用也减弱,图13为沿轴线方向上气流压力的变化情况。其中横坐标表示轴线方向长度,纵坐标表示相对压力,参考压力为101 325 Pa。
图13 不同运行速度下气流通道内部轴线上压力分布

Fig.13 Pressure distribution on the internal axis of the airflow channel at different operating speeds

Full size|PPT slide

从图13中可以看出,进口壁面作用会形成膨胀波,从而导致气流的压力上升。当运行速度为1.5Ma时,相对压力上升峰值为0.14 MPa;运行速度为2Ma时,相对压力上升峰值为0.03 MPa;运行速度为2.5Ma时,相对压力上升峰值为0.025 MPa;运行速度为3Ma时,相对压力上升峰值为0.018 MPa。由此可以看出,随着运行速度的增加,膨胀波的压力增强效应逐渐减弱。

2.3 试验验证

为确认气流通道设计的正确性,开展火箭橇试验验证。试验中火箭橇在发动机推力下做加速运动,当运行至特定速度(710 m/s)时,启动橇载解锁装置,气流扩张装置在气动力作用下绕转轴向内旋转,扩张比由2.2变化至4.5,通过锁定机构将其固定,随后橇体在空气阻力作用下减速滑行,直至停止。采用上述试验方法,在相同火箭橇运行速度下通过增大扩张比,获得更高速度的试验环境,从而实现变马赫的目的。采用空速管、静压传感器测量气流通道内流场马赫数和静压,并与仿真数据进行对比。空速管选在上子午线两侧,距被试品头部210 mm处,空速管1为左偏15°,空速管2为右偏15°,左、右侧子午线上各布设3个静压传感器,第1个静压传感器距被试品头部282 mm,每隔48 mm布设1个静压传感器,如图14所示。
图14 测试元件布设图

Fig.14 Layout diagram of test components

Full size|PPT slide

如图15所示,通过地面测试设备获得火箭橇“静止状态—加速运动段—减速滑行段”运行速度随时间的变化曲线,空速管采集了马赫数随时间的变化情况,将若干个特定运行速度下流场均匀区域最大马赫数仿真值与空速管测试结果进行对比,其中均匀区域最大马赫数是通过选取马赫数云图中红色区域靠近被试品多个节点位置马赫数的平均值,不同扩张比下火箭橇运行速度与试验区域最大马赫数仿真值对应关系如表1所示。
图15 验证试验空速管仿真试验对比

Fig.15 Comparison of simulation and reality of airspeed tube test data in verification test

Full size|PPT slide

表1 不同扩张比下火箭橇运行速度与试验区域最大马赫数仿真值对应关系

Table 1 Corresponding relationship between the running speed of the rocket sled and the simulation value of the maximum Mach number in the test area under different expansion ratios

Expansion
ratio		 Running
speed/Ma		 Maximum Mach
number/Ma
2.2 357 2.06
2.2 476 2.63
2.2 544 2.65
2.2 612 2.92
2.2 680 3.20
2.2 710 3.27
4.5 710 3.62
4.5 748 3.72
由图15可知,火箭橇最大运行速度为748m/s时,气流扩张通道内最高马赫数为3.72,试验测试最高马赫数为3.58,偏差为3.9%。由表1可以看出,运行速度为710 m/s时,扩张比由2.2变为4.5,试验区域最大马赫数由3.27瞬间增至3.62,实现了变马赫数的目的。
同理,6个静压测试点试验值与仿真值的对比曲线如图16所示,坐标0 s是从火箭橇静止状态开始计时的。由图16可知,对6个静压测点仿真及试验数据进行统计,偏差在6.5%以内,一致性较好。
图16 静压测点仿真试验一致性对比曲线

Fig.16 Comparison curve of simulated consistency of static pressure measurement points

Full size|PPT slide

3 结论

对火箭橇高超声速环境模拟试验的气流扩张通道装置进行设计与数值模拟,结果表明:
1)扩张通道内部主要分为初始源流膨胀区、消波区和均匀流试验区,初始膨胀段型线可采用Foelsch方法设计,过渡消波段则采用基于预设轴线马赫数的特征线方法设计;
2)通道进口膨胀波随着运行速度的增加而减弱,使气流进口条件得到改善,数值分析结果表明,气流扩张通道3Ma速度条件的相对压力峰值比1.5Ma速度条件的相对压力峰值下降87%;
3)文中设计的气流扩张通道可准确模拟高空连续变马赫气流环境,为国内冲压发动机、超声速无人机等武器装备研制提供了一种有效的地面动态试验方法。

参考文献

列表( 原文顺序 | 文献年度倒序 | 文中引用次数倒序 ) 可视化分析
[1]
肖军, 耿强, 徐进欣, 等. 常规兵器火箭橇试验速度影响因素分析[J]. 兵器装备工程学报, 2021, 42(3): 83-87.
XIAO J, GENG Q, XU J X, et al. Analysis of factors influencing the speed of conventional weapon rocket sled test[J]. Journal of Ordnance Equipment Engineering, 2021, 42(3): 83-87.
本文引用 [1]
[2]
夏有财, 孙其会, 肖军, 等. 火箭橇运动计算算法优化与试验验证[J]. 航空动力学报, 2021, 36(7): 1564-1568.
XIA Y C, SUN Q H, XIAO J, et al. Optimization and experimental verification of rocket sled motion calculation algorithm[J]. Journal of Aerospace Power, 2021, 36(7): 1564-1568.
本文引用 [1]
[3]
余元元, 叶俊杰, 张雨诗, 等. 火箭橇轨道系统瞬态动力学特性研究[J]. 兵器装备工程学报, 2019, 40(12): 205-209.
YU Y Y, YE J J, ZHANG Y S, et al. Research on transient dynamic characteristics of rocket sled track system[J]. Journal of Ordnance Equipment Engineering, 2019, 40(12): 205-209.
本文引用 [1]
[4]
汪运鹏, 姜宗林. 高超声速喷管设计理论与方法[J]. 力学进展, 2021, 51(2): 257-294.
WANG Y P, JIANG Z L. A review of theories and methods for hypersonic nozzle design[J]. Advances in Mechanics, 2021, 51(2): 257-294.
本文引用 [1]
[5]
刘亚洲, 李平, 陈宏玉, 等. 不同延伸段压力分布的双钟形喷管设计[J]. 航空动力学报, 2022, 37(2): 424-432.
LIU Y Z, LI P, CHEN H Y, et al. Design of double bell shaped nozzles with different extension pressure distribution[J]. Journal of Aerospace Power, 2022, 37(2): 424-432.
本文引用 [1]
[6]
ZHOU X W, XU J, LYU S Y. Verification of a ground-based method for simulating high-altitude, supersonic flight conditions[J]. International Journal of Computational Materials Science and Engineering, 2018, 7(1): 1850005.
本文引用 [1]
[7]
王英鹏, 徐义华, 孙海俊, 等. 基于响应面法的火箭发动机喷管型面优化设计[J]. 航空动力学报, 2022, 37(1): 214-224.
WANG Y P, XU Y H, SUN H J, et al. Optimization design of rocket engine nozzle profile based on response surface methodology[J]. Journal of Aerospace Power, 2022, 37(1): 214-224.
本文引用 [1]
[8]
陈以勒, 俞凯凯, 徐惊雷. 几何尺寸约束的超燃冲压发动机推力喷管设计[J]. 航空学报, 2021, 42(6): 253-263.
CHEN Y L, YU K K, XU J L. Design of thrust nozzle for scramjet engine with geometric dimension constraints[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(6): 253-263.
本文引用 [1]
[9]
FOELSCH K. The analytical design of an axially symmetric laval nozzle for a parallel and uniform jet[J]. Journal of the Aeronautical Sciences, 1948, 16: 161-188.
本文引用 [1]
[10]
SIVELLS J C. Aerodynamic design of axisymmetric hypersonic wind-tunnel nozzles[J]. Journal of Spacecraft, 1970, 7: 1292-1299.
本文引用 [1]
[11]
张亚林, 李晓松. 改进AOA结合贝塞尔曲线平滑的机器人路径规划[J]. 计算机工程与设计, 2023, 44(10): 3170-3178.
ZHANG Y L, LI X S. Improving robot path planning by combining AOA with bessel curve smoothing[J]. Computer Engineering and Design, 2023, 44(10): 3170-3178.
本文引用 [1]
[12]
张晨辉, 徐健. 火箭橇试验战斗部动态攻角交互式计算与验证[J]. 弹箭与制导学报, 2020, 40(2): 89-92.
ZHANG H, XU J. Interactive calculation and verification of dynamic attack angles of rocket sled test subjects[J]. Journal of Projectiles, Rockets, Missile and Guidance, 2020, 40 (2): 89-92.
本文引用 [1]

PDF(5392 KB)

31

Accesses

0

Citation

Detail
段落导航
相关文章
版权所有 © 《弹箭与制导学报》编辑部
地址：西安市丈八东路10号　
邮编：710065　
电话：029-88293184，029-88293167　
E-mail：djxb1980@163.com
技术支持：北京玛格泰克科技发展有限公司

/

〈 〉