攻角对超空泡射弹波浪环境入水影响研究

鹿麟, 王辰, 闫雪璞, 高词松, 胡彦晓

弹箭与制导学报 ›› 2023, Vol. 43 ›› Issue (6) : 69-78.

PDF(11079 KB)
中文  |  English
文章检索
高级检索
弹箭与制导学报
PDF(11079 KB)
弹箭与制导学报 ›› 2023, Vol. 43 ›› Issue (6) : 69-78. DOI: 10.15892/j.cnki.djzdxb.2023.06.012

攻角对超空泡射弹波浪环境入水影响研究

作者信息 +

Research on Influence of Attack Angle on Water-entry Trajectory Characteristics of Supercavitation Projectiles in Wave Environment

Author information +
文章历史 +

摘要

为获取超空泡射弹不同攻角入水时的空泡演化与运动特性变化规律,基于RANS方程、Schnerr-Sauer空化模型、k-ε湍流模型,采用重叠网格技术,针对入水速度400 m/s不变,入水攻角不同时,静水与波浪环境下的超空泡射弹入水过程开展了数值模拟研究。研究结果表明:攻角大于2°时,弹丸将在入水过程中出现尾拍现象,尾拍时尾翼划破空泡壁,会造成空泡在此区域的扩张,并对弹道稳定性产生不利影响;尾拍现象发生时,阻力系数和升力系数均会上升,且攻角越大,上升的幅值越大;在波浪环境下,弹丸入水过程中仍然会发生尾拍运动,但与静水环境相比,在尾拍发生的时间上有一定区别。攻角为正时尾拍出现的时间提前,反之则尾拍出现的时间延后。

Abstract

To obtain the water-entry cavitation evolution and motion characteristics of supercavitation projectiles in different attack angle, the water-entry process of constant water-entry speed and different attack angle in hydrostatic and wave environment is simulated by using RANS equation, k-ε turbulence model, Schnerr-Sauer cavitation model and overset mesh. The result shows that the projectile will have an obvious tail-slap phenomenon in the process of water-entry when the attack angle is larger than 2°. When tail-slap phenomenon occurs, the tail wing cuts through the cavity wall, which cause the expansion of the cavity in this area and adversely affect the trajectory stability. Furthermore, both the drag and lift coefficients will rise, and the higher the angle of attack, the greater the rise. In the wave environment, the tail-slap phenomenon will still occur in the process of the projectile entering the water, but compared with the static water environment, there is a certain difference in the time of the tail-slap. When the attack angle is positive, the time of the tail-slap is advanced, otherwise it will be delayed.

关键词

超空泡 / 入水攻角 / 波浪环境 / 空泡演化 / 运动特性 / 数值模拟

Key words

supercavitation / water-entry attack angle / wave environment / cavitation evolution / motion characteristic / numerical simulation

引用本文

EndNote

Ris (Procite)

Bibtex

导出引用
鹿麟, 王辰, 闫雪璞, 等. 攻角对超空泡射弹波浪环境入水影响研究[J]. 弹箭与制导学报, 2023, 43(6): 69-78 https://doi.org/10.15892/j.cnki.djzdxb.2023.06.012
LU Lin, WANG Chen, YAN Xuepu, et al. Research on Influence of Attack Angle on Water-entry Trajectory Characteristics of Supercavitation Projectiles in Wave Environment[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2023, 43(6): 69-78 https://doi.org/10.15892/j.cnki.djzdxb.2023.06.012
中图分类号： TJ012.3 (外弹道学)   

0 引言

在超空泡射弹高速入水过程中,弹丸表面会被空泡完全包裹,发生超空化现象,以减小弹丸所受阻力。依靠该技术,超空泡射弹在入水航行一段时间后仍可维持较高速度,实现对水下目标的精确打击,因此受到了多国学者的高度重视。在超空泡射弹的发射过程中,不可避免的存在着初始扰动,运动方向与弹丸轴向将会存在一个夹角,使得弹丸带攻角入水。入水攻角较大时,空泡将不能完全包裹住弹丸,出现明显的沾湿与尾拍现象,进而影响入水的弹道稳定性。此外,自然界中完全静止的水面并不存在,水面必然存在着波浪,受波浪的影响,弹丸的空泡形态与运动轨迹均将发生变化,使入水过程更加复杂。因此,针对超空泡射弹入水过程开展研究,更加符合武器作战的实际情况,具有重要的学术和军事价值。
近年来,国内外学者针对超空泡射弹入水问题开展了较为深入的研究。在国外,Neaves等[1]对速度420 m/s的射弹入水可压缩多相流进行了模拟,给出了空泡形态以及阻力随时间变化的规律; Truscott等[2]基于空泡截面独立扩张原理研究了高速运动体斜入水问题,结果表明大长径比的运动体具有更好的入水弹道稳定性;Nguyen等[3]采用6DOF理论与自由面流动模型,分析了不同材质与入水速度对运动体入水特性的影响;Mirzaei等[4]提出了可以预测圆柱入水阶段的空泡形态、深闭合以及水花的颈缩现象的数值模型。在国内,黄闯等[5]对运动体入水过程中的空泡形态演变及弹道特性进行了数值研究,并分析了液体可压缩性对空泡的影响;温俊生等[6]计算了平头、圆头、尖头弹以100 m/s速度入水时的空泡形态;陈晨等[7]对运动体高速入水问题进行了数值模拟研究,并总结了入水过程的流体动力特性、流场结构特性与空泡发展特性;秦杨、钱铖铖等[8-9]分析了不同入水角度下超空泡射弹高速倾斜入水特性;李强等[10-11]分析了超空泡射弹结构参数、运动参数对入水流场特性及弹道稳定性的影响;汪振等[12]研究了弹丸高速入水时的冲击载荷变化规律。
以上研究都是在静水环境中开展的,在公开文献与资料中,更贴合实际的波浪环境入水问题研究却甚少,并且现有研究大都集中在对波浪环境的导弹、鱼雷和UUV等大型结构物入水问题的研究上[13⇓⇓-16],但波浪环境同样会影响对超空泡射弹的入水过程。因此,采用重叠网格技术,对静水与波浪环境下,超空泡射弹在不同攻角入水时的空泡演化与运动特性的变化规律开展了研究,相关研究成果可以为提高两栖枪械的有效射程和射击精度提供一定的参考。

1 数学模型选取

1.1 控制方程

超空泡射弹的入水过程包含了水、水蒸气以及空气3种流动介质,属于典型的多相流问题,因此需要考虑多相流模型,采用VOF模型处理多相流动,并假设液体不可压缩,其连续性方程、动量守恒方程分别为:
∂(αqρq)∂t+Δ·(αqρqv)=0
(1)
式中:下标q取v,l,g,分别代表水蒸气、水和空气;αq表示各相的体积分数,且αv+αl+αg=1;ρq表示各相密度;t为时间;v为速度矢量;Δ为Hamilton微分算子。
∂∂t(ρv)+Δ·(ρv2)=-Δp+Δ·(μ(Δv+ΔvT))
(2)
式中:p为流体压力;μ为动力粘度。

1.2 湍流模型

以Standard k-ε模型作为湍流模型[14],其方程式为:
∂∂t(ρκ)+ ∂∂xi(ρκui)= ∂∂xjμ+μtσκ-ρ u'iu'j¯∂uj∂xi-ρε
(3)
∂∂t(ρε)+ ∂∂xi(ρεui)= ∂∂xjμ+μtσε∂ε∂xj-Cε2ρ ε2κ+Cε1 εκρ u'iu'j¯∂uj∂xi
(4)
式中:κ,ε分别为湍流动能和耗散率;σκ,σε分别为κ和ε的湍流普朗特常数,通常取σκ=1.0,σε=1.3;Cε1,Cε2分别为经验系数,通常取 Cε1=1.44,Cε2=1.92。

1.3 空化模型

采用Schnerr-Sauer空化模型以考虑水的空化过程,其方程式为:
∂∂t(αvρv)+Δ·(αvρvvv)=Re-Rc
(5)
Re= ρvρlραv(1-αv) 3rB23(pv-pρl),pv>p
(6)
Rc= ρvρlραv(1-αv) 3rB23(p-pvρl),pv<p
(7)
式中:Re为蒸发速率;Rc为冷凝速率;vv为水蒸气相的速度矢量;rB为气核的半径;pv为水的饱和蒸汽压。

1.4 波浪模型

由于采用的超空泡射弹的口径较小,数值波浪水池的深度和波浪高度均比较小,因此选择一阶正弦波便可满足计算要求,其波面方程和速度势函数分别为:
η= H2cos(ky-ωt)
(8)
ϕ= gH2ω cosh(z+d)cosh(kd)sin(ky-ωt)
(9)
而波数k与圆频率ω色散关系,波长λ与波浪周期T关系分别为:
ω2g=ktan(kd)
(10)
λ= g2πT2tanh 2πλd
(11)
x方向,z方向速度分别为:
ux= gHK2ω cosh(z+d)cosh(kd)cos(ky-ωt)
(12)
uz= gHK2ω sinh(z+d)cosh(kd)sin(ky-ωt)
(13)
式中:H为波浪高度;λ为波浪长度;k为波数,k=2π/λ;y代表与波浪行进方向相同的横向坐标;z代表纵向坐标;ω为波浪圆频率,ω=2π/T,T代表波浪周期;d为静止水面水深。

2 计算模型设置

2.1 几何模型

超空泡射弹模型的外形结构示意图如图1所示,弹丸所用材料为钢,质量为19.4 g,主要由圆锥空化器、圆台段、圆柱段和尾翼4部分组成。超空泡射弹的结构参数与运动参数定义如图2所示,其中,弹丸总长度L=73 mm,圆锥空化器锥角为90°,圆柱段直径R=7.62 mm,尾翼直径Rm=12 mm。定义入水速度为V0,V0与弹丸轴线的夹角为入水攻角α,图中所示方向为正攻角,反之则为负攻角,V0与自由液面的夹角为入水角度θ;并定义图中弹体首先触水的左侧为迎水面,右侧为背水面。
图1 结构参数示意图

Fig.1 Structural parameters

Full size|PPT slide

图2 运动参数示意图

Fig.2 Motion parameters

Full size|PPT slide

2.2 网格划分与计算域设置

采用ANSYS ICEM软件对全计算域进行了结构化网格划分。如图3(a)所示,计算域可分为弹丸子域、加密背景域以及外围区域3大部分。其中加密背景域和弹丸子域采用较密网格以提高计算精度,最大网格尺寸设置为2 mm,而外围区域网格设置较疏,最大网格尺寸设置为5 mm,以提高计算速度。如图3(b)所示,对弹丸附近的网格进行了加密处理以提高精度。对于文中的k-ε湍流模型,参考ANSYS FLUENT的帮助文件,Y+值应大于30。故将第一边界层的网格厚度设为0.003 mm。全计算域的网格总数约为120万。
图3 网格划分示意图

Fig.3 Mesh generation of computational domain

Full size|PPT slide

2.3 边界条件与算法设置

图4给出了文中采用的计算域边界条件设置示意图。其计算域为2 000 mm×500 mm×250 mm的长方体,为减少计算量,采用1/2计算域,在对称面上设置对称面边界条件;计算域侧面分别为速度入口和压力出口,并采用边界造波法生成波浪环境,不设置边界造波且速度入口的速度为0时则为静水环境;其他边界设置为壁面条件。通过三自由度模型计算弹丸运动过程中的速度、位移等运动参数,采用重叠网格技术实现网格更新,并采用PISO算法处理速度与压力耦合。
图4 边界条件设置

Fig.4 Boundary condition setting

Full size|PPT slide

2.4 数值方法验证与网格无关性验证

为验证文中数值方法的有效性,开展了超空泡射弹入水实验,实验系统与弹丸模型示意图如图5所示。实验系统主要由敞口水箱、发射系统、高速摄影系统以及照明系统4部分组成。弹丸口径为7.62 mm,弹丸长度为63 mm,材质为钢,弹重为17.10 g。弹丸的入水角度设置为60°,入水速度设置为120 m/s。
图5 实验系统与弹丸模型示意图

Fig.5 Experiment system layout and projectile model

Full size|PPT slide

与实验工况对应的计算域设置及网格划分如图6所示。弹丸的材料、尺寸与图5中的实验弹丸均保持一致。初始时刻弹丸位于空气域中,入水速度及入水角度与实验同样保持一致。图7和图8分别为实验结果与计算结果的对比图,从图7可以看出,计算所得的入水空泡形态与实验结果基本吻合;从图8可以看出,弹丸在入水过程中的速度衰减曲线也较为相似,最大误差为5.7%。
图6 计算域设置与网格划分

Fig.6 Calculation domain setting and mesh generation

Full size|PPT slide

图7 计算与实验的空泡形态对比图

Fig.7 Comparison of cavition between calculation and experiment

Full size|PPT slide

图8 计算与实验的速度衰减曲线对比图

Fig.8 Comparison of velocity attenuation curve between calculation and experiment

Full size|PPT slide

将网格总数分别设置为90万、120万、150万,以弹丸入水速度V0=400 m/s,入水角度θ=90°工况为例,开展网格无关性验证。图9为计算所得弹丸速度随时间变化曲线,可以看出90万网格弹丸速度衰减略快,而120万网格与150万网格的弹丸速度衰减规律几乎完全一致,因此选择120万网格进行超空泡射弹入水问题的研究。
图9 网格无关性验证结果

Fig.9 Grid independence verification results

Full size|PPT slide

3 计算结果分析

分别针对静水与波浪环境下,攻角不同时的超空泡射弹入水过程开展了数值模拟研究,计算工况详见表1。
表1 计算工况表

Table 1 Calculation working condition table

Parameter Calm environment Wave environment
Initial velocity/(m/s) 400 400
Attack angle/(°) 1,2,3,4 2,-2,4,-4

3.1 攻角对静水环境下入水特性的影响分析

3.1.1 入水流场特性分析

图10为入水速度400 m/s,运动0.4 ms时,超空泡射弹在不同入水攻角下的密度云图。可以看出,各工况的空泡开口处的形态是基本一致的,但由于空泡的轮廓基本为抛物线,当攻角不同时,弹身附近的空泡形态有所不同。通过尾翼附近的放大图可以看出,α=1°和α=2°工况由于攻角较小,空泡对称性较好,尾翼被空泡完全包裹;对于α=3°工况,虽然攻角有所增加,但空泡尚能包裹弹身,尾翼处仅有极小区域沾湿;而α=4°工况的攻角最大,在尾翼位置出现了大范围的沾湿现象。这说明α=4°工况的弹丸尾翼在入水较短时间后时便受到两侧不对称的水动力,这会对之后的入水运动轨迹产生影响。
图10 t=0.4 ms时不同入水攻角下的密度云图

Fig.10 Density contours of different attack angles at 0.4 ms

Full size|PPT slide

图11为运动0.4 ms时,不同攻角下弹丸附近的压力云图以及弹尖附近的放大图。可以看出,高压区在弹尖均呈半球形分布,且随着攻角的增加,弹尖处压力分布越来越不对称,迎水面的压力明显大于背水面的压力,而弹尖两侧压力分布的不均导致了水动力的不均,这也是入水初期弹丸出现偏转力的原因。α取1°,2°,3°,4°时的弹尖处的压力最大值分别为97.8 MPa,92.5 MPa,89.4 MPa,88.1 MPa,可以看出,随着攻角的增大,弹尖处的压力最大值逐渐减小,这是由于攻角越大,弹尖与水的接触面积越大造成的。
图11 t=0.4 ms时不同攻角下弹丸附近的压力云图

Fig.11 Pressure of different attack angles near projectile at 0.4 ms

Full size|PPT slide

图12为运动0.8 ms时,不同攻角下的密度云图。可以看出,对于α=1°工况,弹丸附近的空泡对称性较好,使弹丸可以在水下维持稳定的运动;对于α=2°工况,由上文的分析可知,在弹尖位置处由于压力分布不均,从刚入水时刻起便对弹尖产生了不对称的水动力,进而使弹丸偏转角较刚入水时有所增大;对于α=3°工况,弹丸偏转程度更大,沾湿情况已经与α=4°工况在0.4 ms时的情况相似,尾翼与圆柱段均发生沾湿,弹丸即将发生尾拍;对于α=4°工况,图中圆圈处为尾翼沾湿的运动区域,该区域的空泡直径较其他3种工况有所提高。此外,还可以发现空泡开口处的直径较其他3种工况也有一定程度的增加,这是因为该工况下尾翼刚入水时便沾湿,弹丸传递给周围水的能量更大,进而使自由液面处空泡扩张程度增加。
图12 t=0.8 ms时不同入水攻角下的密度云图

Fig.12 Density contours of different attack angles at 0.8 ms

Full size|PPT slide

3.1.2 入水运动特性分析

图13为不同入水攻角下的Y向弹道偏移量随时间的变化曲线。可以看出,α=1°时弹道偏移量较小,能够在水下稳定运行。而α取2°,3°,4°工况由于出现了尾拍现象,弹道稳定性较差。由3.1.1节的分析可知攻角越大,发生第一次为尾拍的时间越早,因此α=4°工况在1.6 ms左右偏移量达到最大值4.2 mm,随后由于尾翼处回转力的作用弹道偏移量开始逐渐减小。而α取2°,3°工况发生尾拍的时间更晚,在2.5 ms以后的弹道偏移量才开始下降。由于Y正方向运动时间更长,因此与α=4°工况相比在尾拍之前积累了更多的弹道偏移量,最大值均在6 mm左右。
图13 不同入水攻角下Y向弹道偏移量随时间的变化曲线

Fig.13 Variation of Y direction offset of different attack angles

Full size|PPT slide

图14为不同入水攻角下的偏转角随时间变化曲线。
图14 不同入水攻角下的偏转角随时间变化曲线

Fig.14 Variation of deflection angles of different attack angles

Full size|PPT slide

可以看出,从运动开始至0.4 ms,α取2°,3°,4°工况的偏转角均增大,这是因为弹体还未完全入水,尾翼尚在空气中,因此只有弹头处不对称的水动力影响着偏转角,造成了3种工况下弹丸的偏转角均增大。在运动0.4 ms左右,α=4°工况的尾翼进入水中并立刻触碰到空泡边界发生尾拍现象,产生的回转力使弹丸的偏转角迅速减小。对于α=3°工况,0.4 ms尾翼入水时尚未沾湿,而是在继续运动到0.6 ms左右才发生尾拍现象,偏转角也随之减小。对于α=2°工况,初始偏转角最小,尾翼触碰到空泡边界所需的时间最长,因此偏转角在0.8 ms才开始减小。对比α取2°,3°,4°工况还可以发现,弹丸发生第一次尾拍时所需的最小偏转角为3.8°,而α=4°在未入水时偏转角便已超过了这一数值,并且在尾翼入水时偏转角达到了4.2°,因此尾翼处沾湿现象较其他两工况更明显,产生的回转力更大,偏转角下降的速度更快。
为分析超空泡射弹入水过程中的流体动力特性,需要定义阻力系数Ca以及升力系数Cb,其计算公式为:
Ca= 2FaρV2A
(14)
Cb= 2FbρV2A
(15)
式中:Fa为弹丸在速度方向上受到的阻力;Fb为弹丸在与运动速度垂直方向上受到的阻力;ρ为流体密度;V为弹丸运动速度;A为弹体最大横截面积。
图15为不同入水攻角下的阻力系数随时间变化曲线。可以看出,α=1°工况在刚入水时受到冲击作用,阻力系数迅速增大,随后由于空泡的产生阻力系数逐渐下降,并趋于平缓。而其他工况在弹丸入水后阻力系数均出现一定的波动,可以看出阻力系数激增的时刻与尾拍发生的时刻几乎一致,这说明尾拍现象会造成更大的阻力系数出现,进而对超空泡射弹的存速性能产生不利影响。对比阻力系数峰值,可以发现,第一次尾拍时α=2°和α=3°工况的阻力系数峰值近似,均在0.061左右;α=4°工况的阻力峰值最大,达到0.69。这是因为尾拍时的沾湿面积将影响阻力系数峰值,如图14所示,α=2°和α=3°在尾拍时刻的偏转角均为3.8°,而α=4°工况有着更大的偏转角4.2°,其沾湿面积更大,因此阻力系数峰值更大;同时,各工况第二次尾拍时阻力系数峰值较第一次均有提升,这与图14的结论相同,是由于第二次尾拍时偏转角较第一次更大导致的。
图15 不同入水攻角下阻力系数随时间变化曲线

Fig.15 Variation of drag coefficient in different attack angles

Full size|PPT slide

图16为不同入水攻角下升力系数随时间变化曲线。可以看出,由于α=1°工况几乎不受到径向力的作用,因此计算时间内的升力系数在0附近振荡。对于α取2°,3°,4°工况,将图15的阻力系数曲线与图16的升力系数曲线对比分析,可以发现是阻力系数与升力系数出现激增的时刻基本一致的,且第二次激增的幅度均大于第一次激增,这说明尾拍现象将同时影响着阻力系数与升力系数的变化。
图16 不同入水攻角下升力系数随时间变化曲线

Fig.16 Variation of lift coefficient in different attack angles

Full size|PPT slide

3.2 攻角对波浪环境下入水特性的影响分析

对于3.1节的工况,超空泡射弹在静水环境垂直入水时,攻角的正负方向对计算结果并无影响。但是在波浪环境中垂直入水时,由于存在波浪方向,正攻角入水与负攻角入水所受的波浪力干扰情况是不同的。因此设置入水角度θ=90°,入水速度V0=400 m/s不变,将入水攻角分别设置为2°,-2°,4°,-4°;采用边界造波法,参考二级海况,设置波高为0.1 m,波长为0.2 m,水流速度为5 m/s;网格数量与第2节相同,并对边界条件进行了改动,如图17所示,以探究入水攻角对超空泡射弹波浪环境入水特性的影响。
图17 边界造波示意图

Fig.17 Boundary wave generation method

Full size|PPT slide

3.2.1 入水流场特性分析

若不加以特殊说明,图中的波浪方向均为从左向右。图18为运动0.3 ms时,不同攻角下的超空泡射弹入水密度云图。图19为该时刻弹体表面的水的体积分数云图。从图18可以看出,在入水初期,攻角的正负对波浪环境超空泡射弹的空泡形态影响相对较小,α=2°与α=-2°工况均为弹丸先接触水的一侧空泡尺寸小于另一侧,α=4°与α=-4°工况下空泡的不对称性更加明显,弹体的圆柱段均出现了沾湿,这一现象在静水工况中也同样出现。有所不同的是,由于α=4°工况中弹体出现沾湿的一侧同时是迎流面,在波浪的作用下,这一侧的空泡扩张受到抑制的程度要更大,因此对比图19(b)和图19(d)可以看出,α=4°工况中弹体圆柱段的沾湿面积要略大于α=-4°工况,这将使α=4°工况的弹丸在入水初期受到更为不对称的水动力作用。
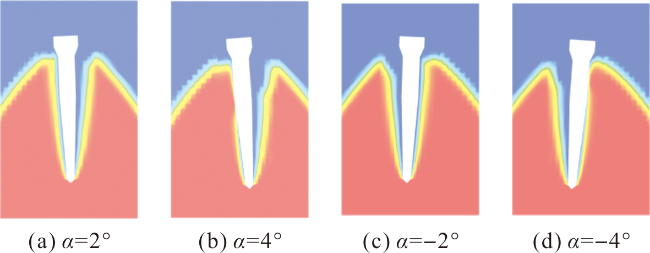
图18 t=0.3 ms时不同攻角下的入水密度云图

Fig.18 Density contours of different attack angles at 0.3 ms

Full size|PPT slide

图19 t=0.3 ms时弹体表面水的体积分数云图

Fig.19 Liquid fraction of different attack angles at 0.3 ms

Full size|PPT slide

图20为运动0.3 ms时,弹尖附近的压力云图,波浪方向仍为从左向右。
图20 t=0.3 ms时弹尖附近的压力云图

Fig.20 Pressure contours near projectile at 0.3 ms

Full size|PPT slide

可以看出,随着攻角的增大,弹尖与水的接触面积增大,因此高压区的范围也随之增大,且迎水面与背水面的压力不对称性也明显增大,这一结论对于静水环境不同攻角的工况也同样成立。对比图20(a)与(c),以及图20(b)与(d),可以发现只改变攻角的方向而不改变大小时,弹尖附近的压力云图没有明显的区别,这说明在本节的工况中,弹尖处产生不对称水动力的主要原因是攻角的出现,攻角越大则弹尖所受径向水动力越大,而波浪力的作用对弹尖的影响于攻角而言相对较小。
图21为运动1.6 ms时,不同攻角下的超空泡射弹入水密度云图。可以看出,主要受攻角的影响,各工况的弹丸在入水后均发生了尾拍现象,与静水工况相同的是,在尾拍的位置处由于尾翼的二次空化,空泡出现了过度扩张的情况。对比空泡过度扩张的位置,可以发现攻角大小相同但正负不同时,正攻角的工况发生空泡扩张的位置要明显早于负攻角的工况,这说明弹丸在正攻角下的入水空泡受到波浪的影响更大,弹丸也更容易发生尾拍现象。综合3.1.1节与3.2.1节进行分析,对于入水速度V0=400 m/s,入水角度θ=90°的工况,入水攻角不变的情况下,静水与波浪环境下的超空泡射弹的入水空泡演化过程近似。但由于波浪对空泡的干扰,攻角为正时尾拍提前,攻角为负时尾拍延后。
图21 t=1.6 ms时不同攻角下的密度云图

Fig.21 Density contours of different attack angles at 1.6 ms

Full size|PPT slide

3.2.2 入水运动特性分析

图22为不同入水攻角下Y向弹道偏移量随时间的变化曲线。可以看出对于攻角较大的α=4°与α=-4°工况,在运动0.5 ms时完成第一次尾拍,弹道偏移量开始有了明显增加。α=4°工况在1.67 ms时弹道偏移量达到了最大值5.44 mm,而α=-4°工况在1.94 ms时偏移量达到了最大值5.08 mm。由此可知,在攻角大小相同的情况下,正攻角弹丸入水弹道偏移量的增速要明显大于负攻角弹丸,且到达偏移量最大值的时间将会提前,这一现象在α=2°与α=-2°工况的对比中同样可以体现。这是因为如3.1节中所分析的,在弹丸以正攻角入水时,先入水的一侧处于迎流面,在波浪的干扰下空泡扩张受到更加明显抑制的作用,弹丸沾湿的程度更大,因此弹丸受到了更大的Y负方向波浪力作用,加速了弹丸偏转。而负攻角入水时主要为背流面弹体沾湿,沾湿区域没有受到波浪力的额外作用,因此弹道偏移量相对较小。此外,无论是正攻角工况还是负攻角工况,攻角越大时,弹道偏移量的第一次峰值到达的时间越短,与静水工况下的现象相同。
图22 不同入水攻角下Y向弹道偏移量随时间的变化曲线

Fig.22 Variation of Y direction offset of different attack angles

Full size|PPT slide

图23为不同入水攻角下的偏转角随时间变化曲线。可以看出,在弹丸刚入水至运动0.5 ms时,各工况由于弹尖处受水动力不对称偏转角均小幅度增加,但由于这一阶段持续时间较短,在图23中弹道偏移量没有明显的改变。各工况在运动0.5 ms时尾翼入水,α=4°与α=-4°工况均达到了尾拍时所需的偏转角,随后发生尾拍且偏转角开始减小;而α=2°与α=-2°的偏转角则继续增加,分别在0.99 ms和1.38 ms的偏转角才达到最大值,这与图22同样反应了正攻角入水时,尾拍发生的时间会提前。综合图22与图23可知,以负攻角入水的弹丸,在波浪环境的弹道稳定性要好于相同大小以正攻角入水的弹丸。
图23 不同入水攻角下的偏转角随时间变化曲线

Fig.23 Variation of deflection angles of different attack angles

Full size|PPT slide

图24为不同入水攻角下的阻力系数随时间变化曲线。可以看出,波浪环境各工况在弹尖刚入水时的阻力系数峰值均要大于静水工况的0.06,尤其是α=4°与α=-4°工况,阻力系数峰值分别达到了0.09和0.08,由于α=4°工况的迎水面与波浪水流的接触面积更大,因此有着更大的阻力系数。α=4°工况不只在入水的阻力系数峰值上更大,在0.5 ms第一次发生尾拍时的阻力系数同样大于其他工况,这也是因为该工况在尾拍时的沾湿面积更大造成的。此外,各工况第二次尾拍时偏转角较第一次更大,所以第二次尾拍的阻力系数峰值也更大。将图24与图15中静水环境的对应工况进行比较,可以发现对于同一运动参数下的弹丸,在波浪环境入水时,虽然弹体被空泡完全包裹时阻力系数无明显区别,但发生尾拍时有着更大的阻力系数,这必将对弹丸的存速产生不利影响。
图24 不同入水攻角下的阻力系数随时间变化曲线

Fig.24 Variation of drag coefficient in different attack angles

Full size|PPT slide

图25为不同入水攻角下的升力系数随时间变化曲线。可以看出,从运动开始到0.5 ms的时间内,各工况的升力系数无明显变化。在弹丸运动0.5 ms时,α=4°与α=-4°工况由于尾翼沾湿而出现尾拍现象,升力系数明显上升,且α=4°的升力系数峰值更大。而α=2°与α=-2°工况在此刻偏转角相对较小,分别在1 ms和1.5 ms才出现升力系数的上升。对比图24和图25可以看出,同一工况在入水之后阻力系数与升力系数出现上升的时刻基本一致,其原因与静水工况相同,也是由于尾拍现象造成的,这里不再重复分析。
图25 不同入水攻角下的升力系数随时间变化曲线

Fig.25 Variation of lift coefficient in different attack angles

Full size|PPT slide

4 结论

采用重叠网格技术,对静水与波浪环境下,入水速度400 m/s不变,入水攻角不同时的超空泡射弹入水过程开展了数值模拟研究,获得以下主要结论:
1)入水攻角大于2°时,弹丸将出现明显的尾拍现象,尾拍时尾翼划破空泡壁,会造成空泡在此区域的扩张,并对弹道稳定性产生不利影响。
2)尾拍现象发生时,阻力系数和升力系数均会上升,且攻角越大,上升的幅值越大,这将同样影响弹丸的存速性能。
3)在波浪环境下,与静水环境相似的是,弹丸入水过程中仍然会发生尾拍运动。但与静水环境相比,在尾拍发生的时间上有一定区别。攻角为正时尾拍出现的时间提前,反之则尾拍出现的时间延后。

参考文献

列表( 原文顺序 | 文献年度倒序 | 文中引用次数倒序 ) 可视化分析
[1]
NEAVES M D, EDWARDS J R. All-speed time-accurate underwater projectile calculations using a reconditioning algorithm[J]. Journal of Fluids Engineering, 2006, 128(2): 284-296.
本文引用 [1]
[2]
TRUSCOTT T T, EPPS B P, BELDEN J. Water entry of projectiles[J]. Annu Rev Fluid Mech, 2014, 46(1): 355-378.
本文引用 [1]
[3]
NGUYEN V T, PHAN T H, DUY T N, et al. 3D simulation of water entry of an oblique cylinder with six-degree-of-freedom motions using an efficient free surface flow model[J]. Ocean Engineering, 2021: 108409.
本文引用 [1]
[4]
MIRZAEI M, TAGHVAEI H, GOLNESHAN A A. Improvement of cavity shape modeling in water-entry of circular cylinders by considering the cavity memory effect[J]. Applied Ocean Research, 2020, 97: 102073.
本文引用 [1]
[5]
黄闯, 罗凯, 白杰, 等. 液体可压缩性对超空化流动的影响[J]. 上海交通大学学报, 2016, 50(8): 1241-1245.
HUANG C, LUO K, BAI J, et al. Influence of liquid's compressibility on supercavitating flow[J]. Journal of Shanghai Jiao Tong University, 2016, 50(8): 1241-1245.
本文引用 [1]
[6]
温俊生, 施红辉, 徐胜利, 等. 头型对回转体垂直入水时空泡面闭合影响的数值模拟[J]. 浙江理工大学学报(自然科学版), 2018, 39(5): 573-579.
WEN J S, SHI H H, XU S L, et al. Numerical simulation of the effect of different head form on surface closure of water entry supercavity[J]. Journal of Zhejiang Institute of Science and Technology(Natural Science Edition), 2018, 39(5): 573-579.
本文引用 [1]
[7]
陈晨, 魏英杰, 王聪, 等. 射弹跨声速入水初期阶段多相流场特性数值研究[J]. 振动与冲击, 2019, 38(6): 46-53.
CHEN C, WEI Y J, WANG C, et al. Numerical analysis of the multiphase flow characteristics in the initial period of water-entry of a projectile at transonic speed[J]. Journal of Vibration and Shock, 2019, 38(6) : 46-53.
本文引用 [1]
[8]
秦杨, 易文俊, 管军. 超空泡枪弹高速倾斜入水的空化流动数值模拟[J]. 兵器装备工程学报, 2019, 40(7): 99-104.
QIN Y, YI W J, GUAN J. Numerical simulation for cavitation flow of high-speed rotating body oblique entrying into water[J]. Journal of Ordnance Equipment Engineering, 2019, 40(7): 99-104.
本文引用 [1]
[9]
钱铖铖, 余春华, 穆青, 等. 发射速度和发射角度对射弹高速入水流动的影响[J]. 兵器装备工程学报, 2019, 40(7): 35-39.
QIAN C C, YUN C H, MU Q, et al. Numerical research of effects of launch speed and launch angle on water entry of high-speed projectile[J]. Journal of Ordnance Equipment Engineering, 2019, 40(7): 35-39.
本文引用 [1]
[10]
LI Q, LU L. Numerical investigations of trajectory characteristics of a high-speed water-entry projectile[J]. Aip Advance, 2020, 10: 95-107.
本文引用 [1]
[11]
LI Q, LU L. Numerical investigations of cavitation nose structure of a high-speed projectile impact on water-entry characteristics[J]. Journal of Marine Science and Engineering, 2020, 8(4): 265.
本文引用 [1]
[12]
汪振, 吴茂林, 戴文留. 大口径弹体高速入水载荷特性研究[J]. 弹道学报, 2020, 32(1): 15-22.
https://doi.org/10.12115/j.issn.1004-499X(2020)01-003
摘要
针对未来海上平台发射大口径抛射体入水冲击载荷问题,为了研究速度接近200 m/s时,不同速度、入水角度以及攻角对大口径平头弹体入水径向载荷以及轴向载荷的影响,基于LS-DYNA软件,采用多介质ALE方法,对速度在150～190 m/s,入水角度在45°～60°之间,具有3°～7°攻角的弹体入水模型进行数值模拟。结果表明:在同一入水速度的情况下,轴向载荷峰值随入水角度的增加而增加,径向载荷峰值随着入水角度的改变有一定的波动; 在入水初期,径向载荷到达峰值后慢慢趋于稳定并收敛于0; 径向载荷的峰值出现在轴向载荷撞水瞬间产生的第1次小峰值时刻; 正攻角会使弹体产生顺时针旋转的径向载荷,负攻角会使弹体产生逆时针旋转的径向载荷,载荷大小随着攻角数值大小的增大而增大。
WANG Z, WU M L, DAI W L. Study on load characteristics of high-speed water-entry of large caliber projectile[J]. Journal of Ballistics, 2020, 32(1): 15-22.
https://doi.org/10.12115/j.issn.1004-499X(2020)01-003
本文引用 [1] 摘要
Aiming at the problem of water entry overload of large caliber projectile launched by offshore platforms in the future,the effects of different velocities,water inflow angles,and angle of yaw on the radial and axial loads of large caliber flat-nosed projectiles with the velocity approaching 200 m/s were studied. Based on LS-DYNA software,the multi-medium Arabic Lagrange Euler(ALE)method was used to simulate the water entry model of a projectile with velocity of 150-190 m/s,water inflow angle of 45°-60° and angle of yaw of 3°-7°. At the same velocity,the peak value of axial load increases with the increase of water entry angle,and the peak value of radial load fluctuates with the change of water entry angle. At the initial stage of water inflow,the radial load gradually stabilizes and converges to zero after reaching its peak value. The peak value of radial load occurs at the first small peak moment when the axial load collides with water. The positive angle of attack will cause the radial load of clockwise rotation,while the negative angle of attack will cause the radial load of counter-clockwise rotation. The magnitude of the load increases with the increase of the numerical value of the angle of attack.
[13]
杨晓光, 党建军, 王鹏, 等. 波面环境对高速入水载荷及弹道特性影响试验研究[J]. 西北工业大学学报, 2021, 39(6): 1259-1265.
YANG X G, DANG J J, WANG P, et al. Experimental research on influence of wave environment on high-speed water entry load and trajectory characteristics[J]. Journal of Northwestern Polytechnical University, 2021, 39(6): 1259-1265.
本文引用 [1]
[14]
SUN S Y, SUN S L, WU G X. Oblique water entry of a wedge into waves with gravity effect[J]. Journal of Fluids and Structures, 2015, 52: 49-64.
本文引用 [2]
[15]
JIN Y, ZHI H, LU Y, et al. Numerical simulation of three dimensional tank impacting on wavy water[C]// AIAA. Proceedings of the AIAA Aviation 2019 Forum. Reston: AIAA, 2019: 3642.
本文引用 [1]
[16]
XIANG G, LI X, YU X, et al. Motion dynamics of dropped cylindrical objects in flows after water entry[J]. Ocean Engineering, 2019, 173: 659-671.
本文引用 [1]

基金

国家自然科学基金(52201385)
山西省自然科学基金(20210302123023)
山西省回国留学人员科研资助项目(2020-106)

PDF(11079 KB)

44

Accesses

0

Citation

Detail
段落导航
相关文章
版权所有 © 《弹箭与制导学报》编辑部
地址：西安市丈八东路10号　
邮编：710065　
电话：029-88293184，029-88293167　
E-mail：djxb1980@163.com
技术支持：北京玛格泰克科技发展有限公司

/

〈 〉